Bisectors of the angles B and C of

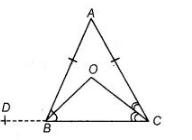
Given $\triangle A B C$ is an isosceles triangle in which $A B=A C, B O$ and $C O$ are the bisectors of

$\angle A B C$ and $\angle A C B$ respectively intersect at $O$.

To show $\angle D B A=\angle B O C$

Construction Line CB produced to $D$.

Proof In $\triangle A B C$, $A B=A C$   [given]

$\angle A C B=\angle A B C$

[angles opposite to equal sides are equal]

$\Rightarrow \quad \frac{1}{2} \angle A C B=\frac{1}{2} \angle A B C \quad$ [on dividing both sides by 2]

$\Rightarrow \quad \angle O C B=\angle O B C$ ......(i)

$[\because B O$ and $C O$ are the bisectors of $\angle A B C$ and $\angle A C B]$

In $\triangle B O C, \angle O B C+\angle O C B+\angle B O C=180^{\circ}$     [by angle sum property of a triangle]

$\Rightarrow$ $\angle O B C+\angle O B C+\angle B O C=180^{\circ}$ [from Eq. (i)]

$\Rightarrow$ $2 \angle O B C+\angle B O C=180^{\circ}$

$\Rightarrow$ $\angle \mathrm{ABC}+\angle \mathrm{BOC}=180^{\circ}$ $[\because B O$ is the bisector of $\angle A B C]$

$\Rightarrow$ $180^{\circ}-\angle D B A+\angle B O C=180^{\circ}$ $[\because D B C$ is a straight line] 

$\Rightarrow$ $-\angle D B A+\angle B O C=0$

$\Rightarrow$ $\angle D B A=\angle B O C$