At the foot of a mountain, the angle of elevation of its summit is $45^{\circ}$. After ascending 1 km towards the mountain up an incline of $30^{\circ}$
the elevation changes to $60^{\circ}$ (as shown in the given figure). Find the height of the mountain. [Given $: \sqrt{3}=1.73]$
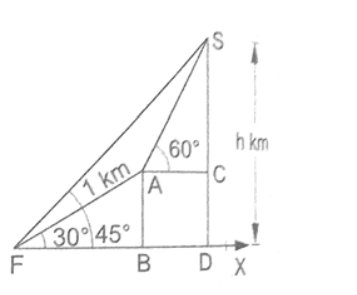
After ascending $1 \mathrm{~km}$ towards the mountain up an incline of $30^{\circ}$, the elevation changes to $60^{\circ}$
So, according to the figure given, $A B=A F \times \sin 30^{\circ}=(1 \times 0.5)=0.5 \mathrm{Km}$.
At point $A$ the elevation changes to $60^{\circ}$.
In this figure, $\Delta_{\mathrm{ABF}} \cong \Delta_{\mathrm{ACS}}$
Comparing these triangles, we get $A B=A C=0.5 \mathrm{Km}$
Now, $\mathrm{CS}=\mathrm{AC} \times \tan 60^{\circ}=(0.5 \times 1.73)=0.865 \mathrm{Km}$
Therefore, the total height of the mountain is $=C S+D C$
$=C S+B A$
$=(0.865+0.5) \mathrm{Km}$
$=1.365 \mathrm{Km}$
