Assertion (A)
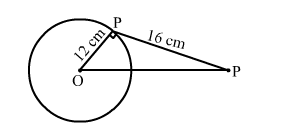
At point P of a circle with centre O and radius 12 cm, a tangent PQ of length 16 cm is drawn. Then, OQ = 20 cm.
Reason (R)
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
(c) Assertion (A) is true and Reason (R) is false.
(d) Assertion (A) is false and Reason (R)is true.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
In $\Delta O P Q, \angle O P Q=90^{\circ}$.
$\therefore O Q^{2}=O P^{2}+P Q^{2}$
$\Rightarrow O Q=\sqrt{O P^{2}+P Q^{2}}$
$=\sqrt{12^{2}+16^{2}}$
$=\sqrt{144+256}$
$=\sqrt{400}$
$=20 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.