As observed from the top of a 75 m tall light house,

Let $O C$ be the height of light house $75 \mathrm{~m}$. and $A$ and $B$ the position of two ships and angle of depression are $A=30^{\circ}$ and $B=45^{\circ}$. Let $O C=75$ and $B C=h, A B=x$

Here we have to find distance between two ships.

The corresponding figure is as follows

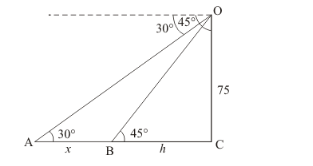
So we trigonometric ratios,

In ΔOBC

$\Rightarrow \quad \tan 45^{\circ}=\frac{O C}{B C}$

$\Rightarrow \quad 1=\frac{75}{h}$

$\Rightarrow \quad h=75$

Again in $\triangle O A C$

$\Rightarrow \quad \tan 30^{\circ}=\frac{O C}{A B+B C}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{75}{x+h}$

$\Rightarrow \quad x+h=75 \sqrt{3}$

$\Rightarrow \quad x+75=75 \sqrt{3}$

$\Rightarrow \quad y=75(\sqrt{3}-1)$

Hence distance between two ships is $75(\sqrt{3}-1) \mathrm{m}$.