As observed form the top of a lighthouse, 100 m above sea level,

Solution:

Let $O A$ be the lighthouse and $B$ and $C$ be the two positions of the ship.

Thus, we have:

$O A=100 \mathrm{~m}, \angle O B A=30^{\circ}$ and $\angle O C A=60^{\circ}$

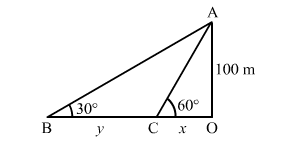
Let:

$O C=x \mathrm{~m}$ and $B C=y \mathrm{~m}$

In the right $\triangle O A C$, we have:

$\frac{O A}{O C}=\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \frac{100}{x}=\sqrt{3}$

$\Rightarrow x=\frac{100}{\sqrt{3}} \mathrm{~m}$

Now, in the right $\Delta O B A$, we have:

$\frac{O A}{O B}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{100}{x+y}=\frac{1}{\sqrt{3}}$

$\Rightarrow x+y=100 \sqrt{3}$

On putting $x=\frac{100}{\sqrt{3}}$ in the above equation, we get:

$y=100 \sqrt{3}-\frac{100}{\sqrt{3}}=\frac{300-100}{\sqrt{3}}=\frac{200}{\sqrt{3}}=115.47 \mathrm{~m}$

$\therefore$ Distance travelled by the ship during the period of observation $=B C=y=115.47 \mathrm{~m}$