Question:
Area lying in the first quadrant and bounded by the circle $x^{2}+y^{2}=4$ and the lines $x=0$ and $x=2$ is
A. $\pi$
B. $\frac{\pi}{2}$
C. $\frac{\pi}{3}$
D. $\frac{\pi}{4}$
Solution:
The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as
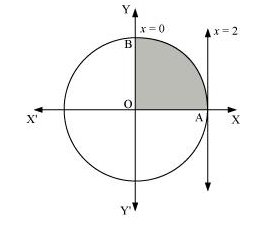
$\therefore$ Area $\mathrm{OAB}=\int_{0}^{2} y d x$
$=\int_{0}^{2} \sqrt{4-x^{2}} d x$
$=\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}\right]_{0}^{2}$
$=2\left(\frac{\pi}{2}\right)$
$=\pi$ units
Thus, the correct answer is A.
