Question:
Area lying between the curve $y^{2}=4 x$ and $y=2 x$ is
A. $\frac{2}{3}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{3}{4}$
Solution:
The area lying between the curve, $y^{2}=4 x$ and $y=2 x$, is represented by the shaded area $\mathrm{OBAO}$ as
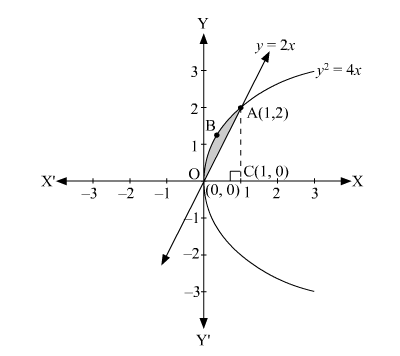
The points of intersection of these curves are O (0, 0) and A (1, 2).
We draw AC perpendicular to x-axis such that the coordinates of C are (1, 0).
∴ Area OBAO = Area (OCABO) – Area (ΔOCA)
$=\int_{0}^{1} 2 \sqrt{x} d x-\int_{0}^{1} 2 x d x$
$=2\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{1}-2\left[\frac{x^{2}}{2}\right]_{0}^{1}$
$=\left|\frac{4}{3}-1\right|$
$=\frac{1}{3}$ square units
Thus, the correct answer is B.
