Question:
Ap unbiased coin is tossed 5 times. Suppose that a variable
$X$ is assigned the value $k$ when $k$ consecutive heads are obtained for $k=3,4,5$, otherwise $X$ takes the value $-1$.
Then the expected value of $X$, is:
Correct Option: , 2
Solution:
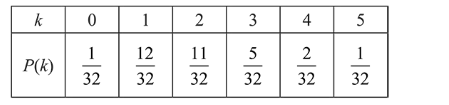
$k=$ No. of times head occur consecutively
Now expectation
$=\sum x P(k)=(-1) \times \frac{1}{32}+(-1) \times \frac{12}{32}+(-1) \times \frac{11}{32}$
$+3 \times \frac{5}{32}+4 \times \frac{2}{32}+5 \times \frac{1}{32}=\frac{1}{8}$
