Question:
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given
figure). Show that AP || BQ.
Solution:
Given In the figure l || m, AP and BQ are the bisectors of ∠EAB and ∠ABH, respectively.
To prove AP|| BQ
Proof Since, l || m and t is transversal.
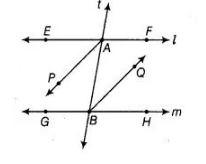
½ ∠EAB =½ ∠ABH [dividing both sides by 2]
∠PAB =∠ABQ
[AP and BQ are the bisectors of ∠EAB and ∠ABH] Since, ∠PAB and ∠ABQ are alternate interior angles with two lines AP and BQ and transversal
AB. Hence, AP || BQ.
Therefore, ∠EAB = ∠ABH [alternate interior angles]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.