An observer 1.5 m tall is 30 m away from a chimney.

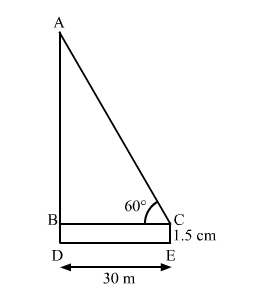
Let CE and AD be the heights of the observer and the chimney, respectively.

We have,

$\mathrm{BD}=\mathrm{CE}=1.5 \mathrm{~m}, \mathrm{BC}=\mathrm{DE}=30 \mathrm{~m}$ and $\angle \mathrm{ACB}=60^{\circ}$

In $\triangle \mathrm{ABC}$,

$\tan 60^{\circ}=\frac{\mathrm{AB}}{\mathrm{BC}}$

$\Rightarrow \sqrt{3}=\frac{\mathrm{AD}-\mathrm{BD}}{30}$

$\Rightarrow \mathrm{AD}-1.5=30 \sqrt{3}$

$\Rightarrow \mathrm{AD}=30 \sqrt{3}+1.5$

$\Rightarrow \mathrm{AD}=30 \times 1.732+1.5$

$\Rightarrow \mathrm{AD}=51.96+1.5$

$\Rightarrow \mathrm{AD}=53.46 \mathrm{~m}$

So, the height of the chimney is 53.46 m (approx.).