An observed from the top of a 150 m tall light house, the angles of depression

Solution:

Let  be the light house of  m. and angle of depression of two ship C and D are  and  respectively.

Let, $B C=x, C D=y$ and $\angle A D B=30^{\circ}, \angle A C B=45^{\circ}$.

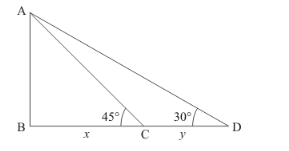
We use trigonometric ratios.

In a triangle,

$\Rightarrow \tan 45^{\circ}=\frac{A B}{B C}$

$\Rightarrow 1=\frac{150}{x}$

$\Rightarrow x=150$

Again in a triangle,

$\Rightarrow \tan 30^{\circ}=\frac{A B}{B D}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{150}{x+y}$

$\Rightarrow x+y=150 \sqrt{3}$

$\Rightarrow 150+y=150 \sqrt{3}$

$\Rightarrow y=150 \sqrt{3}-150$

$\Rightarrow y=150(\sqrt{3}-1)$

$\Rightarrow y=150 \times 0.732$

Hence distance between the ships is $109.8 \mathrm{~m}$.