Question:
An object of mass $m_{1}$ collides with another object of mass $\mathrm{m}_{2}$, which is at rest. After the collision the objects move with equal speeds in opposite direction. The ratio of the masses $\mathrm{m}_{2}: \mathrm{m}_{1}$ is:
Correct Option: 1
Solution:
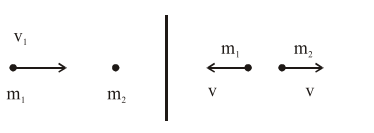
$m_{1} v_{1}=-m_{1} v+m_{2} v$
$v_{1}=-v+\frac{m_{2}}{m_{1}} v$
$\mathrm{v}_{1}=-\mathrm{v}+\frac{\mathrm{m}_{2}}{\mathrm{~m}_{1}} \mathrm{v}$
$\frac{\left(v_{1}+v\right)}{v}=\frac{m_{2}}{m_{1}}$
$\mathrm{e}=\frac{2 \mathrm{v}}{\mathrm{v}_{1}}=1$
$\mathrm{V}=\frac{\mathrm{v}_{1}}{2}$
$\frac{v_{1}+v_{1} / 2}{v_{1} / 2}=\frac{m_{2}}{m_{1}}$
$3=\frac{m_{2}}{m_{1}}$
