An isosceles triangle of vertical angle

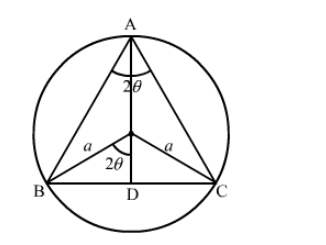
Let $\mathrm{ABC}$ be an isosceles triangle inscribed in the circle with radius a such that $\mathrm{AB}=\mathrm{AC}$.

$\mathrm{AD}=\mathrm{AO}+\mathrm{OD}=a+a \cos 2 \theta=a(1+\cos 2 \theta)$ and

$\mathrm{BC}=2 \mathrm{BD}=2 a \sin 2 \theta$

As, area of the triangle $\mathrm{AC}, A=\frac{1}{2} \mathrm{BC} \times \mathrm{AD}$

$\Rightarrow A(\theta)=\frac{1}{2} \times 2 a \sin 2 \theta \times a(1+\cos 2 \theta)$

$=a^{2} \sin 2 \theta(1+\cos 2 \theta)$

$=a^{2} \sin 2 \theta+a^{2} \sin 2 \theta \cos 2 \theta$

$\Rightarrow A(\theta)=a^{2} \sin 2 \theta+\frac{a^{2} \sin 4 \theta}{2}$

$\Rightarrow A^{\prime}(\theta)=2 a^{2} \cos 2 \theta+\frac{4 a^{2} \cos 4 \theta}{2}$

$\Rightarrow A^{\prime}(\theta)=2 a^{2} \cos 2 \theta+2 a^{2} \cos 4 \theta$

$\Rightarrow A^{\prime}(\theta)=2 a^{2}(\cos 2 \theta+\cos 4 \theta)$

For maxima or minima, $A^{\prime}(\theta)=0$

$\Rightarrow 2 a^{2}(\cos 2 \theta+\cos 4 \theta)=0$

$\Rightarrow \cos 2 \theta+\cos 4 \theta=0$

$\Rightarrow \cos 2 \theta=-\cos 4 \theta$

$\Rightarrow \cos 2 \theta=\cos (\pi-4 \theta)$

$\Rightarrow 2 \theta=\pi-4 \theta$

$\Rightarrow 6 \theta=\pi$

$\Rightarrow \theta=\frac{\pi}{6}$

Also, $A^{\prime \prime}(\theta)=2 a^{2}(-\sin 2 \theta-\sin 4 \theta)=-2 a^{2}(\sin 2 \theta+\sin 4 \theta)<0$ at $\theta=\frac{\pi}{6}$

So, the area of the triangle is maximum at $\theta=\frac{\pi}{6}$.