An inclined plane is bent in such a way that the vertical cross-section is given by $y=\frac{x^{2}}{4}$ where $y$ is in vertical and $x$ in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction $\mu=0.5$, the maximum height in $\mathrm{cm}$ at which a stationary block will not slip downward is $\mathrm{cm}$.
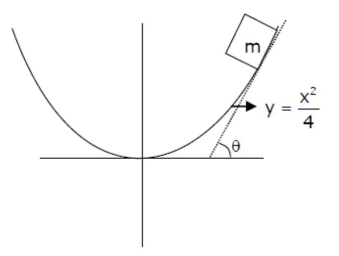
given
$y=\frac{x^{2}}{4}$
$\mu=0.5$
condition for block will not slip downward
$\mathrm{mg} \sin \theta=\mu \mathrm{mg} \cos \theta$

$\Rightarrow \tan \theta=\mu$
and we know that
$\Rightarrow \tan \theta=\frac{d y}{d x}$
$\Rightarrow \frac{d y}{d x}=\mu \Rightarrow \frac{x}{2}=0.5$
$\left[\begin{array}{l}y=\frac{x^{2}}{4} \\ \frac{d y}{d x}=\frac{x}{2}\end{array}\right]$
put $x=1$ in equation $y=x^{2} / 4$
$\Rightarrow y=\frac{(1)^{2}}{4} \Rightarrow y=\frac{1}{4} \Rightarrow y=0.25$
$y=25 \mathrm{~cm}$
