An inclined plane is bent in such a way that the vertical cross-section is given by $y=\frac{x^{2}}{4}$ where $\mathrm{y}$ is in vertical and $\mathrm{x}$ in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction $\mu=0.5$, the maximum height in $\mathrm{cm}$ at which a stationary block will not slip downward is
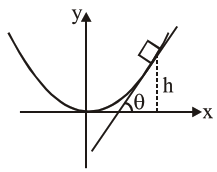
At maximum ht. block will experience maximum friction force. Therefore if at this height slope of the tangent is $\tan \theta$, then $\theta=$ Angle of repose.
$\therefore \tan \theta=\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}=0.5$
$\Rightarrow \mathrm{x}=1$ and therefore $\mathrm{y}=\frac{\mathrm{x}^{2}}{4}=0.25 \mathrm{~m}$
$=25 \mathrm{~cm}$
$\therefore$ Answer is $25 \mathrm{~cm}$
(Assuming that $\mathrm{x}$ \& $\mathrm{y}$ in the equation are given in meter)
