An equilateral triangle of side 9 cm is inscribed in a circle.

(c) $3 \sqrt{3} \mathrm{~cm}$

Let ΔABC be an equilateral triangle of side 9 cm.
Let AD be one of its medians.

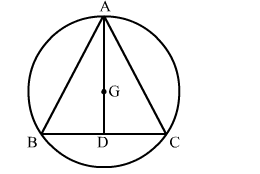
Then AD ⊥ BC and BD = 4.5 cm

$\therefore \mathrm{AD}=\sqrt{\mathrm{AB}^{2}-\mathrm{BD}^{2}}=\sqrt{(9)^{2}-\left(\frac{9}{2}\right)^{2}}=\sqrt{81-\frac{81}{4}}=\sqrt{\frac{324-81}{4}}=\sqrt{\frac{243}{4}}=\frac{9 \sqrt{3}}{2} \mathrm{~cm}$

Let G be the centroid of ΔABC.
Then AG : GD = 2 : 1

$\therefore$ Radius $=\mathrm{AG}=\frac{2}{3} \mathrm{AD}=\left(\frac{2}{3} \times \frac{9 \sqrt{3}}{2}\right) \mathrm{cm}=3 \sqrt{3} \mathrm{~cm}$