An engine operates by taking a monatomic ideal gas through the cycle shown in the figure.

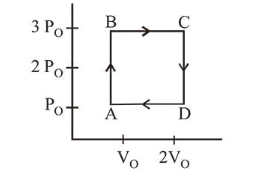
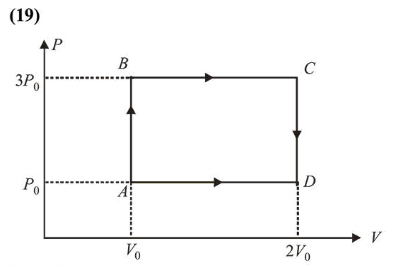
From the figure,

Work, $W=2 P_{0} V_{0}$

Heat given, $Q_{\text {in }}=W_{A B}+W_{B C}=n \cdot C_{V} \Delta T_{A B}+n C_{P} \Delta T_{B C}$

$=n \frac{3 R}{2}\left(T_{B}-T_{A}\right)+\frac{n 5 R}{2}\left(T_{C}-T_{B}\right)$

$\left(\because C_{v}=\frac{3 R}{2}\right.$ and $\left.C_{P}=\frac{5 R}{2}\right)$

$=\frac{3}{2}\left(P_{B} V_{B}-P_{A} V_{A}\right)+\frac{5}{2}\left(P_{C} V_{C}-P_{B} V_{B}\right)$

$=\frac{3}{2} \times\left[3 P_{0} V_{0}-P_{0} V_{0}\right]+\frac{5}{2}\left[6 P_{0} V_{0}-3 P_{0} V_{0}\right]$

$=3 P_{0} V_{0}+\frac{15}{2} P_{0} V_{0}=\frac{21}{2} P_{0} V_{0}$

Efficiency, $\eta=\frac{W}{Q_{\text {in }}}=\frac{2 P_{0} V_{0}}{\frac{21}{2} P_{0} V_{0}}=\frac{4}{21}$

$\eta \%=\frac{400}{21} \approx 19$