An engine is attached to a wagon through a shock absorber of length $1.5 \mathrm{~m}$. The system with a total mass of $40,000 \mathrm{~kg}$ is moving with a speed of $72 \mathrm{kmh}^{-1}$ when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by $1.0 \mathrm{~m}$. If $90 \%$ of energy of the wagon is lost due to friction, the spring constant is $\times 10^{5} \mathrm{~N} / \mathrm{m}$.
Work $=\Delta \mathrm{K} . \mathrm{E}$
$\mathrm{W}_{\text {friction }}+\mathrm{W}_{\text {spring }}=0-\frac{1}{2} \mathrm{mv}^{2}$
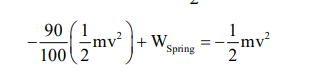
$\mathrm{W}_{\text {spring }}=-\frac{10}{100} \times \frac{1}{2} \mathrm{mv}^{2}$
$-\frac{1}{2} \mathrm{kx}^{2}=-\frac{1}{20} \mathrm{mv}^{2}$
$\Rightarrow \mathrm{k}=\frac{40000 \times(20)^{2}}{10 \times(1)^{2}}=16 \times 10^{5}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.