An aeroplane is flying at a height of 300 m above the ground.

Let CD be the height of the aeroplane above the river at some instant. Suppose A and B be two points on both banks of the river in opposite directions.

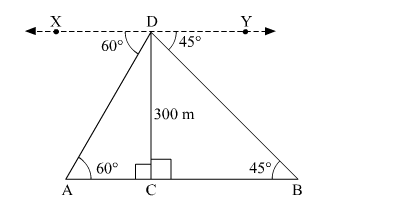
Height of the aeroplane above the river, CD = 300 m
Now,
∠">∠CAD = ∠">∠ADX = 60º       (Alternate angles)
∠">∠CBD = ∠">∠BDY = 45º        (Alternate angles)
In right ∆ACD,

$\tan 60^{\circ}=\frac{\mathrm{CD}}{\mathrm{AC}}$

$\Rightarrow \sqrt{3}=\frac{300}{\mathrm{AC}}$

$\Rightarrow \mathrm{AC}=\frac{300}{\sqrt{3}}=100 \sqrt{3} \mathrm{~m}$

In right ∆BCD,

$\tan 45^{\circ}=\frac{\mathrm{CD}}{\mathrm{BC}}$

$\Rightarrow 1=\frac{300}{\mathrm{BC}}$

$\Rightarrow \mathrm{BC}=300 \mathrm{~m}$

∴ Width of the river, AB

$=B C+A C$

$=300+100 \sqrt{3}$

$=300+100 \times 1.73$

$=300+173$

$=473 \mathrm{~m}$

Thus, the width of the river is 473 m.