An aeroplane flying horizontally 1 km above the ground is observed

An aero plane is flying  km above the ground making an angle of elevation of aero plane 60°. After  seconds angle of elevation is changed to 30°. Let , , , ,km and km. Here we have to find speed of aero plane.

The corresponding figure is as follows

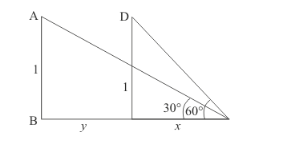
So we use trigonometric ratios.

In $\triangle D C E$

$\Rightarrow \quad \tan 60^{\circ}=\frac{1}{x}$

$\Rightarrow \quad \sqrt{3}=\frac{1}{x}$

$\Rightarrow \quad x=\frac{1}{\sqrt{3}}$

Again in $\triangle A B E$,

$\Rightarrow \quad \tan 30^{\circ}=\frac{1}{x+y}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{1}{x+y}$

$\Rightarrow \quad x+y=\sqrt{3}$

$\Rightarrow \quad y=\sqrt{3}-\frac{1}{\sqrt{3}}$

$\Rightarrow \quad y=\frac{2}{\sqrt{3}}$

speed $=\frac{\text { distance }}{\text { time }}$

$=\frac{y}{10 \mathrm{sec}}$

$=\frac{\frac{2}{\sqrt{3}}}{\frac{10}{60 \times 60}}$

$=415.68$

Hence the speed of aero plane is $415.68 \mathrm{~km} / \mathrm{h}$