Akhila went to a fair in her village. She wanted to enjoy rides in the Giant Wheel and play Hoopla (a game in which you throw a rig on the items kept in the stall, and if the ring covers any object completely you get it.) The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. Each ride costs Rs 3, and a game of Hoopla costs Rs 4. If she spent Rs 20 in the fair, represent this situation algebraically and graphically.
Let no. of ride is $x$ and no. of Hoopla is $y$.He paid Rs 20 for $x$ ride and $y$ for Hoopla.
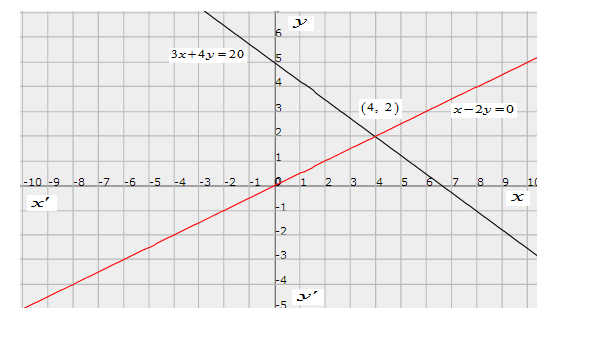
The cost of ride is Rs 3 and cost of Hoopla is Rs 4 . then $3 x+4 y=20$
The number of Hoopla is the half number of ride, then
$\Rightarrow y=\frac{1}{2} x \Rightarrow x-2 y=0$
$3 x+4 y=20$
Hence algebraic equations are $3 x+4 y=20$ and $x-2 y=0$
Now, we draw the graph for algebraic equations.