AC = CO = D, S1 C = S2 C = d << D A small transparent slab containing material of µ =1.5 is placed along AS2. What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
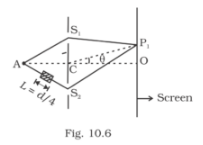
∆x = 2d sin θ+(μ-1)L
sin θ0 = -1/16
From central maxima, OP = -D/16
$\sin \theta_{1}=\frac{\pm \lambda / 2-d / 8}{2 d}$
On the positive side,
$\sin \theta_{1}^{+}=3 / 16$
On the negative side,
$\sin \theta_{1}^{-}=-5 / 16$
The first principal maxima on the positive side is at a distance, which is above point O
$D \tan \theta_{1}^{-}=\frac{3 D}{\sqrt{247}}$
The first principal minima on the negative side is at distance, which is below point O
$D \tan \theta_{1}^{-}=\frac{5 D}{\sqrt{16^{2}-5^{2}}}=\frac{5 D}{\sqrt{231}}$
