ABCDEF is a regular hexagon with centre O (in the following figure).

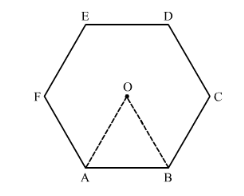
We know that a regular hexagon is made up of 6 equilateral triangles.

We have given area of the one of the triangles.

$\therefore$ Area of the hexagon $=6 \times$ area of one equilateral triangle

$\therefore$ Area of the hexagon $=6 \times 9$

$\therefore$ Area of the hexagon $=54$

We know that if a regular hexagon is inscribed in the circle, then the radius of the circle is same as the side of the regular hexagon.

We also know that a regular hexagon is made up of 6 equilateral triangles and we have area of one of the equilateral triangle.

$\therefore$ Area of the equilateral triangle $=\frac{\sqrt{3}}{4} \times$ side $^{2}$

Substituting the value of the given equilateral triangle we get,

$\therefore 9=\frac{\sqrt{3}}{4} \times$ side $^{2}$

$\therefore$ side $^{2}=\frac{9 \times 4}{\sqrt{3}}$

$\therefore \operatorname{side}^{2}=\frac{36}{\sqrt{3}}$

Now we will find the area of the circle.

$\therefore$ Area of the circle $=\pi r^{2}$

Substituting the values we get,

$\therefore$ Area of the circle $=\frac{22}{7} \times \frac{36}{\sqrt{3}}$

Now we will substitute $\sqrt{3}=1.732$ we get,

$\therefore$ Area of the circle $=\frac{22}{7} \times \frac{36}{1.732}$

$\therefore$ Area of the circle $=\frac{792}{12.124}$

$\therefore$ Area of the circle $=65.324$

Therefore, area of the hexagon and area of the circle are $54 \mathrm{~cm}^{2}$ and $65.324 \mathrm{~cm}^{2}$ respectively.