ABCD is trapezium in which AB || DC,

Given in a trapezium $A B C D, A B \| D C, D C=30 \mathrm{~cm}$ and $A B=50 \mathrm{~cm}$.

Also, $X$ and $Y$ are respectively the mid-points of $A D$ and $B C$.

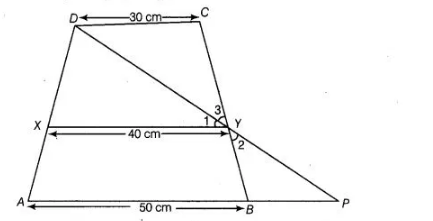
To prove ar $(D C Y X)=\frac{7}{9} \operatorname{ar}(X Y B A)$

Construction Join $D Y$ and extend it to meet produced $A B$ at $P$. Proof $\ln \triangle D C Y$ and $\triangle P B Y$,

$C Y=B Y$  [since, $Y$ is the mid-point of $B C$ ]

$\angle D C Y=\angle P B Y$ [alternate interior angles]

and  $\angle 2=\angle 3$ [vertically opposite angles]

$\therefore \quad \Delta D C Y \cong P B Y$ [by ASA congruence rule]

Then, $D C=B P$ [by CPCT]

But $D C=30 \mathrm{~cm}$ [given]

$\therefore$ $D C=B P=30 \mathrm{~cm}$ 

Now, $A P=A B+B P$

$=50+30=80 \mathrm{~cm}$

In $\triangle A D P$, by mid-point theorem,

$X Y=\frac{1}{2} A P=\frac{1}{2} \times 80=40 \mathrm{~cm}$

Let distance between $A B, X Y$ and $X Y, D C$ is $h \mathrm{~cm}$.

Now, area of trapezium $D C Y X=\frac{1}{2} h(30+40)$

$\left[\because\right.$ area of trapezium $=\frac{1}{2}$ sum of parallel sides $\times$ distance between them]

$=\frac{1}{2} h(70)=35 h \mathrm{~cm}^{2}$

Similarly, area of trapezium $X Y B A=\frac{1}{2} h(40+50)=\frac{1}{2} h \times 90=45 h \mathrm{~cm}^{2}$

$\therefore \quad \frac{\operatorname{ar}(D C Y X)}{\operatorname{ar}(X Y B A)}=\frac{35 h}{45 h}=\frac{7}{9}$

$\Rightarrow \quad \operatorname{ar}(D C Y X)=\frac{7}{9} \operatorname{ar}(X Y B A)$ 

Hence proved.