ABCD is a trapezium with parallel sides AB = a cm and DC = b cm.

(b) Given, $A B=a \mathrm{~cm}, D C=b \mathrm{~cm}$ and $A B \| D C$.

Also, $E$ and $F$ are mid-points of $A D$ and $B C$, respectively.

So, distance between $C D, E F$ and $A B, E F$ will be same say $h$.

Join $B D$ which intersect $E F$ at $M$.

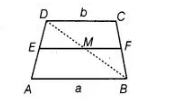
Now, in $\triangle A B D, E$ is the mid-point of $A D$ and $E M \| A B$

So, $M$ is the mid-point of $B D$

and $\quad E M=\frac{1}{2} A B \quad$ [by mid-point theorem] ...(i)

Similarly in $\triangle C B D$,  $M F=\frac{1}{2} C D$ .....(ii)

On adding, Eqs. (i) and (ii), we get

$E M+M F=\frac{1}{2} A B+\frac{1}{2} C D$

$\Rightarrow$ $E F=\frac{1}{2}(A B+C D)=\frac{1}{2}(a+b)$

Now, area of trapezium $A B F E=\frac{1}{2}$ (sum of parallel sides)

$\times$ (distance between parallel sides)

$=\frac{1}{2}\left(a+\frac{1}{2}(a+b)\right) \times h=\frac{1}{4}(3 a+b) h$

Now, area of trapezium $E F C D=\frac{1}{2}\left[b+\frac{1}{2}(a+b)\right] \times h=\frac{1}{4}(3 b+a) h$

$\therefore$ Required ratio $=\frac{\text { Area of } A B F E}{\text { Area of } E F C D}=\frac{\frac{1}{4}(3 a+b) h}{\frac{1}{4}(3 b+a) h}$

$=\frac{(3 a+b)}{(a+3 b)}$ or $(3 a+b):(a+3 b)$