ABCD is a square of side 4 cm.

Solution:

We have the following diagram.

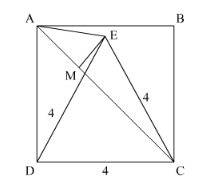
Since $\triangle$ CED is equilateral,

Therefore,

$\mathrm{EC}=\mathrm{CD}=\mathrm{DE}=4 \mathrm{~cm}$

Now, $\angle \mathrm{ECD}=60^{\circ}$

Since AC is diagonal of sqr.ABCD

Therefore,

$\angle \mathrm{ACD}=45^{\circ}$

Therefore we get,

$\angle \mathrm{ECA}=\angle \mathrm{ECD}-\angle \mathrm{ACD}$

$=60^{\circ}-45^{\circ}$

 

$=15^{\circ}$

Now, in $\triangle \mathrm{ACE}$, draw a perpendicular EM to the base AC.

So in $\triangle \mathrm{EMC}$,

$\sin 15^{\circ}=\frac{E M}{E C}$

$=\frac{E M}{4}$

Therefore,

$\mathrm{EM}=\sqrt{2}(\sqrt{3}-1)$

Now in $\triangle \mathrm{AEC}$,

$a r(\triangle \mathrm{AEC})=\frac{1}{2}(\mathrm{AC})(\mathrm{EM})$

$=4(\sqrt{3}-1) \mathrm{cm}^{2}$

So the answer is (b)