Question:
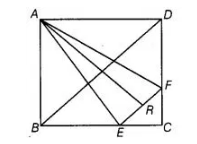
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar (ΔAER) = ar (ΔAFR).
Solution:
Given in square $A B C D, E$ and $F$ are the mid-points of $B C$ and $C D$ respectively. Also, $R$ is the mid-point of $E F$.
To prove $\operatorname{ar}(A E R)=\operatorname{ar}(A F R)$.
Construction Draw $A N \perp E F$
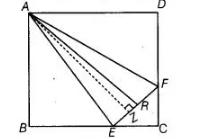
Proof $\because \quad$ ar $(\triangle A E R)=\frac{1}{2} \times$ Base $\times$ Height
$=\frac{1}{2} \times E R \times A N$
$=\frac{1}{2} \times F R \times A N$
$[\because R$ is the mid-point of $E F$, so $E R=F R]$
$=\operatorname{ar}(\Delta \mathrm{AFR})$
Hence proved.
