ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

Solution:



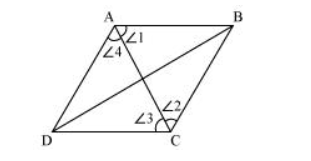
Let us join AC.

In $\triangle \mathrm{ABC}$,

$\mathrm{BC}=\mathrm{AB}$ (Sides of a rhombus are equal to each other)

$\therefore \angle 1=\angle 2$ (Angles opposite to equal sides of a triangle are equal)

However, $\angle 1=\angle 3$ (Alternate interior angles for parallel lines $A B$ and $C D$ )

$\Rightarrow \angle 2=\angle 3$

Therefore, $A C$ bisects $\angle C$.

Also, $\angle 2=\angle 4$ (Alternate interior angles for $\|$ lines $B C$ and $D A$ )

$\Rightarrow \angle 1=\angle 4$

Therefore, $A C$ bisects $\angle A$.

Similarly, it can be proved that $B D$ bisects $\angle B$ and $\angle D$ as well.