ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C.

Solution:

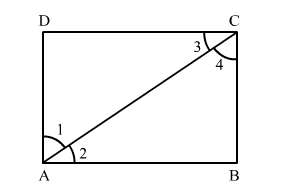
Given: In rectangle ABCD, AC bisects ∠A, i.e. ∠1 = ∠2 and AC bisects ∠C, i.e. ∠3 = ∠4.
 
To prove:
(i) ABCD is a square,
(ii) diagonal BD bisects ∠B as well as ∠D.

Proof:

(i)

Since, $A D \| B C$ (Opposite sides of a rectangle are parallel.)

So, $\angle 1=\angle 4$    (Alternate interior angles)

But, $\angle 1=\angle 2$     (Given)

So, $\angle 2=\angle 4$

In $\Delta A B C$,

Since, $\angle 2=\angle 4$

So, $B C=A B$    (Sides opposite to equal angles are equal.)

But these are adjacent sides of the rectangle ABCD.

Hence, ABCD is a square.

(ii)
Since, the diagonals of a square bisects its angles.
So, diagonals BD bisects ∠B as well as ∠D.