$\mathrm{ABCD}$ is a quadrilateral in which $\mathrm{AB} \| \mathrm{DC}$ and $\mathrm{AD}=\mathrm{BC}$. Prove that $\angle \mathrm{A}=\angle \mathrm{B}$ and $\angle \mathrm{C}=\angle \mathrm{D}$.
Given $A B C D$ is a quadrilateral such that $A B \| D C$ and $A D=B C$
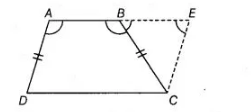
Construction Extend $A B$ to $E$ and draw a line $C E$ parallel to $A D$.
Proof Since, $A D \| C E$ and transversal $A E$ cuts them at $A$ and $E$, respectively.
$\therefore \quad \angle A+\angle E=180^{\circ}$ [since, sum of cointerior angles is $180^{\circ}$ ]
$\Rightarrow \quad \angle A=180^{\circ}-\angle E$ $\ldots(1)$
Since, $A B \| C D$ and $A D \| C E$
So, quadrilateral $A E C D$ is a parallelogram.
$\Rightarrow \quad A D=C E \Rightarrow B C=C E \quad[\because A D=B C$, given $]$
Now, in $\triangle B C E$ $C E=B C$ [proved above]
$\Rightarrow \quad \angle C B E=\angle C E B$
[opposite angles of equal side are equal]
$\Rightarrow \quad 180^{\circ}-\angle B=\angle E \quad\left[\because \angle B+\angle C B E=180^{\circ}\right]$
$\Rightarrow \quad 180^{\circ}-\angle E=\angle B$ ......(ii)
From Eqs. (i) and (ii), $\angle A=\angle B$ Hence proved.
