ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Thinking Process
Firstly, use the property that if two sides of a triangle are equal, then their opposite angles are equal. Further, show that ΔBAD and ΔBCD are
congruent by SAS rule.
Given $A B C D$ is a quadrilateral in which $A B=B C$ and $A D=C D$.
To show $B D$ bisects both the angles $A B C$ and $A D C$.
Proof Since, $A B=B C$ (given)
$\therefore$ $\angle 2=\angle 1$ $\ldots$ (i)
[angles opposite to equal sides are equal]
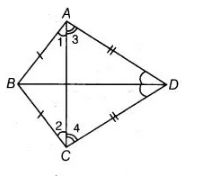
On adding Egs. (0) and (ii), we get
$\angle 2+\angle 4=\angle 1+\angle 3$
$\Rightarrow \quad \angle B C D=\angle B A D \quad \ldots$ (iii)
In $\triangle B A D$ and $\triangle B C D$,
$A B=B C$ [given]
$\angle B A D=\angle B C D$ [from Eq. (iii)]
and $A D=C D$[given]
$\therefore$ $\triangle B A D \cong \triangle B C D$ [by SAS congruence rule]
Hence, $\angle A B D=\angle C B D$ and $\angle A D B=\angle C D B$ i.e., $B D$ bisects the angles $A B C$ and $A D C$.
