$A B C D$ is a parallelogram in which $P$ is the midpoint of $D C$ and $Q$ is a point on $A C$ such that $C Q=\frac{1}{4} A C .$ If $P Q$ produced meets $B C$ at $R$, prove that $R$ is the midpoint $B C$.
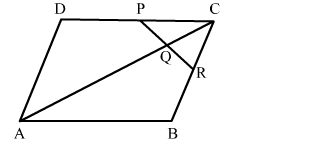
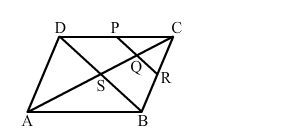
Join DB.
We know that the diagonals of a parallelogram bisect each other.
Therefore
$C S=\frac{1}{2} A C \quad \ldots$ (i)
Also, it is given that $C Q=\frac{1}{4} A C$ ...(ii)
Dividing equation (ii) by (i), we get:
$\frac{C Q}{C S}=\frac{\frac{1}{4} A C}{\frac{1}{2} A C}$
or, $C Q=\frac{1}{2} \operatorname{CS}$
Hence, Q is the midpoint of CS.
Therefore, according to midpoint theorem in $\triangle C S D$
$P Q \| D S$
if $P Q \| D S$, we can say that $Q R \| S B$
In $\triangle C S B, Q$ is midpoint of $C S$ and $Q R \| S B$.
Applying converse of midpoint theorem ,we conclude that R is the midpoint of CB.
This completes the proof.
