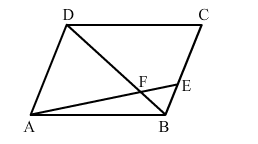
ABCD is a parallelogram and E is a point on BC.

We have: 

$\angle A F D=\angle E F B \quad$ (Vertically Opposite angles)

$\because \mathrm{DA} \| \mathrm{BC}$

$\therefore \angle D A F=\angle B E F \quad$ (Alternate angles)

$\triangle D A F \sim \triangle B E F$               (AA similarity theorem)

$\Rightarrow \frac{A F}{E F}=\frac{F D}{F B}$

or, $A F \times F B=F D \times E F$

This completes the proof.