ABCD is a kite having AB = AD and BC = CD.

Given,

A kite ABCD having AB = AD and BC = CD. P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.

To prove:

PQRS is a rectangle.

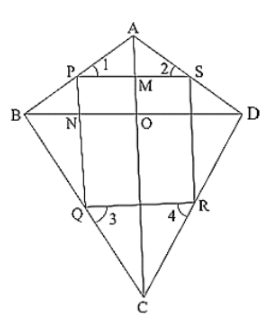
Proof:

In ∆ABC, P and Q are the mid-points of AB and BC respectively.

∴ PQ ∥ AC and PQ = (1/2) AC        .... (i)

In ∆ADC, R and S are the mid-points of CD and AD respectively.

∴ RS ∥ AC and RS = (1/2) AC     .... (ii)

From (i) and (ii) we have

PQ ∥ RS and PQ = RS

Thus, in quadrilateral PQRS, a pair of opposite sides is equal and parallel. So, PQRS is a parallelogram. Now, we shall prove that one angle of parallelogram PQRS is a right angle.

Since AB = AD

⇒12AB = 12AD

⇒ AP = AS      ... (iii)         [∵ P and S are midpoints of AB and AD]

⇒ ∠1 = ∠2             .... (iv)

Now, in ΔPBQ and ΔSDR, we have

PB = SD              [∴ AD = AB ⇒ (1/2) AD = (1/2) AB]

BQ = DR            [Since PB = SD]

And PQ = SR     [Since, PQRS is a parallelogram]

So, by SSS criterion of congruence, we have

ΔPBQ ≅ ΔSDR

⇒∠3 = ∠4 [CPCT]

Now, ⇒ ∠3 + ∠SPQ + ∠2 = 180°

And ∠1 + ∠PSR + ∠4 = 180°

∴ ∠3 + ∠SPQ + ∠2 = ∠1 + ∠PSR + ∠4

⇒ ∠SPQ = ∠PSR               [∠1 = ∠2 and ∠3 = ∠4]

Now, transversal PS cuts parallel lines SR and PQ at S and P respectively.

∴ ∠SPQ + ∠PSR = 180°

⟹ 2∠SPQ = 180°

⟹ ∠SPQ = 90°              [∵ ∠PSR = ∠SPQ]

Thus, PQRS is a parallelogram such that ∠SPQ = 90°.

Hence, PQRS is a parallelogram.