ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y − 5)°,

We know that the sum of the opposite angles of cyclic quadrilateral is $180^{\circ}$ in the cyclic quadrilateral $A B C D$ angles $A$ and $C$ and angles $B$ and $D$ pairs of opposite angles

Therefore

$\angle A+\angle C=180^{\circ}$ and $\angle B+\angle D=180^{\circ}$

$\angle A+\angle C=180^{\circ}$

By substituting $\angle A=(4 y+20)^{\circ}$ and $\angle C=(-4 x)^{\circ}$ we get

$4 y+20-4 x=180^{\circ}$

$-4 x+4 y+20=180^{\circ}$

$-4 x+4 y=180^{\circ}-20$

$-4 x+4 y=160^{\circ}$

$4 x-4 y=-160^{\circ}$

Divide both sides of equation by 4 we get

$x-y=-40^{\circ}$

$x-y+40^{\circ}=0 \cdots(i)$

$\angle B+\angle D=180^{\circ}$

By substituting $\angle B=(3 y-5)^{\circ}$ and $\angle D=(7 x+5)^{\circ}$ we get

$3 y-5+7 x+5=180^{\circ}$

$7 x+3 y=180$

$7 x+3 y-180=0 \cdots(i i)$

By multiplying equation  by 3 we get

$3 x-3 y+120^{\circ}=0 \cdots(i i i)$

By subtracting equation (iii) from (ii) we get

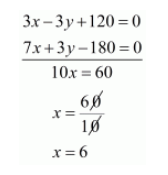
By substituting $x=6^{\circ}$ in equation $(i)$ we get

$x-y+40^{\circ}=0$

$6-y+40=0$

$-1 y=-40-6$

$-1 y=-46$

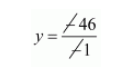
$y=46$

The angles of a cyclic quadrilateral are

$\angle A=4 y+20$

$=4 \times 46+20$

$=184+20$

$=204^{\circ}$

$\angle B=3 y-5$

$=3 \times 46-5$

$=138-5$

$=133^{\circ}$

$\angle C=-4 x^{\circ}$

$=-4(6)$

$=-24^{\circ}$

$\angle D=7 x+5$

$=7 \times 6+5$

$=42+5$

$=47^{\circ}$

Hence the angles of quadrilateral are $\angle A=204^{\circ}, \angle B=133^{\circ}, \angle C=-24^{\circ}, \angle D=47^{\circ}$