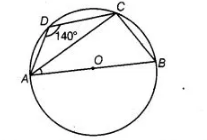
ABCD is a cyclic quadrilateral

Solution:

(b) Given, ABCD is a cyclic quadrilateral and ∠ADC = 140°.

We know that, sum of the opposite angles in a cyclic quadrilateral is 180°.

We know that, sum of the opposite angles in a cyclic quadrilateral is $180^{\circ}$.

$\angle A D C+\angle A B C=180^{\circ}$

$\Rightarrow \quad 140^{\circ}+\angle A B C=180^{\circ}$

$\Rightarrow \quad \angle A B C=180^{\circ}-140^{\circ}$ 

$\therefore \quad \angle A B C=40^{\circ}$

Since, $\angle A C B$ is an angle in a semi-circle.

$\therefore \quad \angle A C B=90^{\circ}$

In $\triangle A B C, \quad \angle B A C+\angle A C B+\angle A B C=180^{\circ}$

[by angle sum property of a triangle]

$\Rightarrow \quad \angle B A C+90^{\circ}+40^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle B A C=180^{\circ}-130^{\circ}=50^{\circ}$