ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥BC (see figure). To prove that ∠BAD = ∠CAD, a student proceeded as
follows
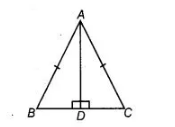
In $\triangle A B D$ and $\triangle A C D$, we have
$A B=A C$ [given]
$\angle B=\angle C$ [because $A B=A C$ ]
and $\angle A D B=\angle A D C$
Therefore, $\triangle A B D \cong \triangle A C D$ [by AAS congruence rule]
So, $\angle B A D=\angle C A D$ [by CPCT]
What is the defect in the above arguments?
In $\triangle A B C$, $A B=A C$
$\Rightarrow \quad \angle A C B=\angle A B C \quad$ [angles oppsoite to the equal sides are equal]
In $\triangle A B D$ and $\triangle A C D$,
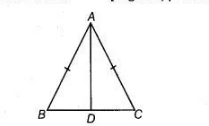
$A B=A C$ [given]
$\angle A B D=\angle A C D$ [proved above]
$\angle A D B=\angle A D C$ [each 90°]
$\therefore$ $\triangle A B D \cong \triangle A C D$[by AAS]
So, $\angle B A D=\angle C A D$ [by CPCT]
So, the defect in the given argument is that firstly prove $\angle A B D=\angle A C D$
Hence, $\angle A B D=\angle A C D$ is defect.
