ABC is an isosceles triangle, right-angled at B.

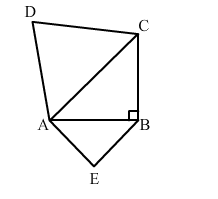
We have, $A B C$ as an isosceles triangle, right angled at $B$.

Now, $\mathrm{AB}=\mathrm{BC}$

Applying Pythagoras theorem in right-angled triangle ABC, we get:

$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}=2 \mathrm{AB}^{2} \quad(\because \mathrm{AB}=\mathrm{AC}) \quad \ldots$ (i)

$\because \triangle \mathrm{ACD} \sim \triangle \mathrm{ABE}$

We know that ratio of areas of 2 similar triangles is equal to squares of the ratio of their corresponding sides.

$\therefore \frac{\operatorname{ar}(\triangle \mathrm{ABE})}{\operatorname{ar}(\triangle \mathrm{ACD})}=\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}[$ from $(\mathrm{i})]$

$=\frac{1}{2}=1: 2$