ABC is an isosceles triangle

Given ΔABC is an isosceles triangle in which AB = AC and BD, CE are its two medians.

To show BD = CE.

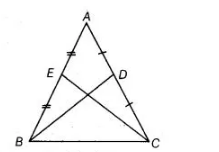
Proof in $\triangle A B D$ and $\triangle A C E$,    $A B=A C$    [given]

$\angle A=\angle A$     [common angle]

and $A D=A E$

$\because$ $A B=A C$

$\Rightarrow$ $\frac{1}{2} A B=\frac{1}{2} A C$

$\Rightarrow$ $A E=A D$

As $D$ is the mid-point of $A C$ and $E$ is the mid-point of $A B$.

$\therefore$ $\triangle A B D \cong \triangle A C E$ [by SAS congruence rule]

$\Rightarrow$ $B D=C E$ [by CPCT]