$\mathrm{ABC}$ is a triangular park with $\mathrm{AB}=\mathrm{AC}=100$ metres. A vertical tower is situated at the mid-point of BC. If the angles of elevation of the top of the tower at $\mathrm{A}$ and $\mathrm{B}$ are $\cot ^{-1}(3 \sqrt{2})$
and $\operatorname{cosec}^{-1}(2 \sqrt{2})$ respectively, then the height of the tower (in metres) is :
Correct Option: , 3
$\cot \alpha=3 \sqrt{2}$
$\& \operatorname{cosec} \beta=2 \sqrt{2}$
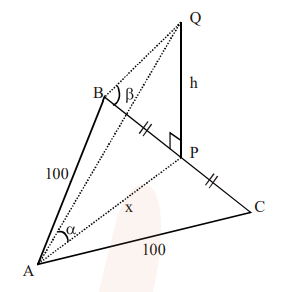
So, $\frac{x}{h}=3 \sqrt{2}$ .............(i)
And $\frac{\mathrm{h}}{\sqrt{10^{4}-\mathrm{x}^{2}}}=\frac{1}{\sqrt{7}}$......(ii)
So, from (i) & (ii)
$\Rightarrow \frac{\mathrm{h}}{\sqrt{10^{4}-18 \mathrm{~h}^{2}}}=\frac{1}{\sqrt{7}}$
$\Rightarrow 25 \mathrm{~h}^{2}=100 \times 100$
$\Rightarrow \mathrm{h}=20 .$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.