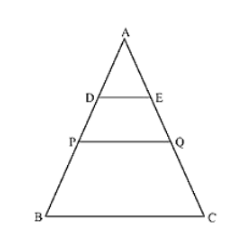
Question:
ABC is a triangle. D is a point on AB such that AD = (1/4) AB and E is a point on AC such that AE = (1/4) AC. Prove that DE = (1/4) BC.
Solution:
Let P and Q be the mid-points of AB and AC respectively.
Then PQ ∥ BC
PQ = (1/2) BC .... (i)
In ΔAPQ, D and E are the mid-points of AP and AQ respectively.
(1/2) DE ∥ PQ, and DE = (1/2) PQ .... (ii)
From (i) and (ii): DE = (1/2) PQ = (1/2) ((1/2) BC)
∴ DE = (1/2) BC
Hence proved.