Solution:
It is given that
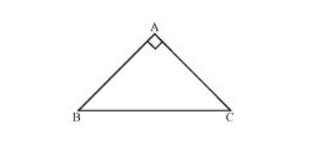
$\mathrm{AB}=\mathrm{AC}$
$\Rightarrow \angle C=\angle B$ (Angles opposite to equal sides are also equal)
$\ln \Delta \mathrm{ABC}$
$\angle A+\angle B+\angle C=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle B+\angle C=180^{\circ}$
$\Rightarrow 90^{\circ}+\angle B+\angle B=180^{\circ}$
$\Rightarrow 2 \angle B=90^{\circ}$
$\Rightarrow \angle B=45^{\circ}$
$\therefore \angle B=\angle C=45^{\circ}$

It is given that
$\mathrm{AB}=\mathrm{AC}$
$\Rightarrow \angle C=\angle B$ (Angles opposite to equal sides are also equal)
$\ln \Delta \mathrm{ABC}$
$\angle A+\angle B+\angle C=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle B+\angle C=180^{\circ}$
$\Rightarrow 90^{\circ}+\angle B+\angle B=180^{\circ}$
$\Rightarrow 2 \angle B=90^{\circ}$
$\Rightarrow \angle B=45^{\circ}$
$\therefore \angle B=\angle C=45^{\circ}$
