Δ ABC and Δ PQR are similar triangles

It is given that there are two similar triangles, $\triangle A B C$ and $\triangle P Q R$ in which $\angle A=32^{\circ}$ and $\angle R=65^{\circ}$, then we have to find $\angle B$ We have following two similar triangles.

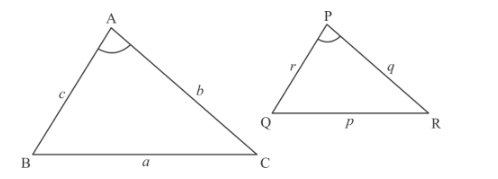
We know the relation between angles in the two similar triangles and these are

$\angle A=\angle P=32^{\circ}$

$\angle C=\angle R=65^{\circ}$

$\angle B=\angle Q$

In $\triangle A B C$ we have,

$\angle A+\angle B+\angle C=180^{\circ}$

$\Rightarrow 32^{\circ}+\angle B+65^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle B=83^{\circ}$

Hence the correct option is $(a)$