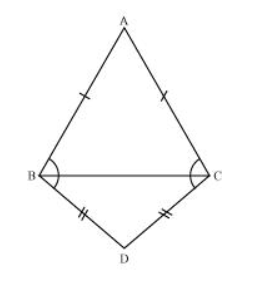
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that ∠ABD = ∠ACD.

Solution:



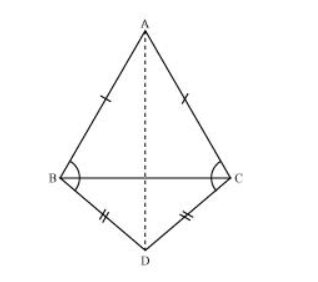
Let us join AD.

In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{ACD}$

$\mathrm{AB}=\mathrm{AC}$ (Given)

BD = CD (Given)

$A D=A D$ (Common side)

$\therefore \triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}$ (By SSS congruence rule)

$\Rightarrow \angle \mathrm{ABD}=\angle \mathrm{ACD}(\mathrm{By} \mathrm{CPCT})$