Question.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Solution:
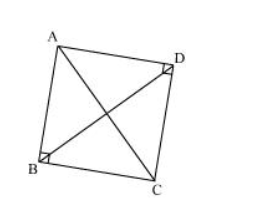
In $\triangle \mathrm{ABC}$,
$\angle A B C+\angle B C A+\angle C A B=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle B C A+\angle C A B=180^{\circ}$
$\Rightarrow \angle B C A+\angle C A B=90^{\circ} \ldots(1)$
In $\triangle \mathrm{ADC}$
$\angle C D A+\angle A C D+\angle D A C=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle A C D+\angle D A C=180^{\circ}$
$\Rightarrow \angle A C D+\angle D A C=90^{\circ} \ldots(2)$
Adding equations (1) and (2), we obtain
$\angle B C A+\angle C A B+\angle A C D+\angle D A C=180^{\circ}$
$\Rightarrow(\angle B C A+\angle A C D)+(\angle C A B+\angle D A C)=180^{\circ}$
$\angle B C D+\angle D A B=180^{\circ}$
However, it is given that
$\angle B+\angle D=90^{\circ}+90^{\circ}=180^{\circ} \ldots(4)$
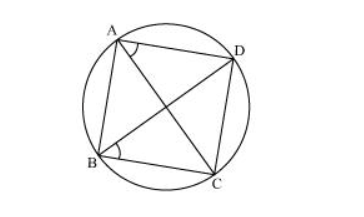
From equations (3) and (4), it can be observed that the sum of the measures of opposite angles of quadrilateral ABCD is 180°. Therefore, it is a cyclic quadrilateral.
Consider chord CD.
$\angle C A D=\angle C B D$ (Angles in the same segment)

In $\triangle \mathrm{ABC}$,
$\angle A B C+\angle B C A+\angle C A B=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle B C A+\angle C A B=180^{\circ}$
$\Rightarrow \angle B C A+\angle C A B=90^{\circ} \ldots(1)$
In $\triangle \mathrm{ADC}$
$\angle C D A+\angle A C D+\angle D A C=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow 90^{\circ}+\angle A C D+\angle D A C=180^{\circ}$
$\Rightarrow \angle A C D+\angle D A C=90^{\circ} \ldots(2)$
Adding equations (1) and (2), we obtain
$\angle B C A+\angle C A B+\angle A C D+\angle D A C=180^{\circ}$
$\Rightarrow(\angle B C A+\angle A C D)+(\angle C A B+\angle D A C)=180^{\circ}$
$\angle B C D+\angle D A B=180^{\circ}$
However, it is given that
$\angle B+\angle D=90^{\circ}+90^{\circ}=180^{\circ} \ldots(4)$
From equations (3) and (4), it can be observed that the sum of the measures of opposite angles of quadrilateral ABCD is 180°. Therefore, it is a cyclic quadrilateral.
Consider chord CD.
$\angle C A D=\angle C B D$ (Angles in the same segment)

