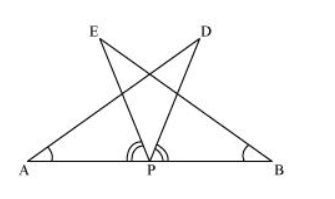
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that<br/><br/>(i) $\triangle \mathrm{DAP} \cong \triangle \mathrm{EBP}$<br/><br/>(ii) $A D=B E$

Solution:

It is given that $\angle E P A=\angle D P B$

$\Rightarrow \angle E P A+\angle D P E=\angle D P B+\angle D P E$

$\Rightarrow \angle \mathrm{DPA}=\angle \mathrm{EPB}$

In $\Delta$ DAP and $\Delta$ EBP,

$\angle \mathrm{DAP}=\angle \mathrm{EBP}($ Given $)$

$\mathrm{AP}=\mathrm{BP}(\mathrm{P}$ is mid-point of $\mathrm{AB})$

$\angle \mathrm{DPA}=\angle \mathrm{EPB}($ From above $)$

$\therefore \triangle \mathrm{DAP} \cong \triangle \mathrm{EBP}(\mathrm{ASA}$ congruence rule $)$

$\therefore \mathrm{AD}=\mathrm{BE}(\mathrm{By} \mathrm{CPCT})$