AB and AC are two chords of a circle of radius r such that AB = 2AC.

Let AC = a.
Since, AB = 2AC, ∴ AB = 2a.

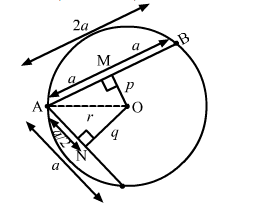
From centre O, perpendicular is drawn to the chords AB and AC at points M and N, respectively.

It is given that OM = p and ON = q.

We know that perpendicular drawn from the centre to the chord, bisects the chord.

∴ AM = MB = a                     ...(1)

and $A N=N C=\frac{a}{2}$         ...(2)

In ∆OAN,

$(A N)^{2}+(N O)^{2}=(O A)^{2}$            (Pythagoras theorem)

$\Rightarrow\left(\frac{a}{2}\right)^{2}+(q)^{2}=(r)^{2}$

$\Rightarrow \frac{a^{2}}{4}+q^{2}=r^{2}$

$\Rightarrow \frac{a^{2}+4 q^{2}}{4}=r^{2}$

$\Rightarrow a^{2}+4 q^{2}=4 r^{2}$

$\Rightarrow a^{2}=4 r^{2}-4 q^{2} \quad \ldots(3)$

In ∆OAM,

$(A M)^{2}+(M O)^{2}=(O A)^{2} \quad$ (Pythagoras theorem)

$\Rightarrow(a)^{2}+(p)^{2}=(r)^{2}$

$\Rightarrow a^{2}=r^{2}-p^{2} \quad \ldots(4)$

From eq. (3) and (4),

$4 r^{2}-4 q^{2}=r^{2}-p^{2}$

$\Rightarrow 4 r^{2}-r^{2}+p^{2}=4 q^{2}$

$\Rightarrow 3 r^{2}+p^{2}=4 q^{2}$

Hence, $4 q^{2}=p^{2}+3 r^{2}$