A wooden article was made by scooping out a hemisphere from each end of a cylinder, as shown in the figure.

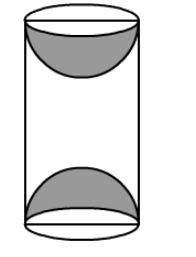
The height h of cylinder = 20 cm and diameter of its base = 7 cm.

$\Rightarrow$ The radius $r$ of its base $=3.5 \mathrm{~cm}$.

$\Rightarrow$ Curved surface area of cylinder $=2 \pi r h=2 \times \frac{22}{7} \times 3.5 \times 20=440 \mathrm{~cm}^{2}$.

Now, curved surface area of one hemisphere $=2 \pi r^{2}=2 \times \frac{22}{7} \times(3.5)^{2}=77 \mathrm{~cm}^{2}$

Total surface area of the article = Curved surface area of cylinder + 2(curved surface area of hemisphere)

$=440+2(77)=440+154=594 \mathrm{~cm}^{2}$