A window is in the form of rectangle surmounted by a semicircular opening.

Let x and y be the length and breadth of the rectangular window.

Radius of the semicircular opening $=\frac{x}{2}$

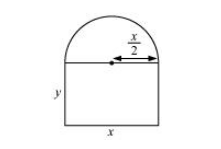
It is given that the perimeter of the window is 10 m.

$\therefore x+2 y+\frac{\pi x}{2}=10$

$\Rightarrow x\left(1+\frac{\pi}{2}\right)+2 y=10$

$\Rightarrow 2 y=10-x\left(1+\frac{\pi}{2}\right)$

$\Rightarrow y=5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)$

∴Area of the window (A) is given by,

$A=x y+\frac{\pi}{2}\left(\frac{x}{2}\right)^{2}$

$=x\left[5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)\right]+\frac{\pi}{8} x^{2}$

$=5 x-x^{2}\left(\frac{1}{2}+\frac{\pi}{4}\right)+\frac{\pi}{8} x^{2}$

$\begin{aligned} \therefore \frac{d A}{d x} &=5-2 x\left(\frac{1}{2}+\frac{\pi}{4}\right)+\frac{\pi}{4} x \\ &=5-x\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4} x \\ \therefore \frac{d^{2} A}{d x^{2}} &=-\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4}=-1-\frac{\pi}{4} \end{aligned}$

Now, $\frac{d A}{d x}=0$

$\Rightarrow 5-x\left(1+\frac{\pi}{2}\right)+\frac{\pi}{4} x=0$

$\Rightarrow 5-x-\frac{\pi}{4} x=0$

$\Rightarrow x\left(1+\frac{\pi}{4}\right)=5$

$\Rightarrow x=\frac{5}{\left(1+\frac{\pi}{4}\right)}=\frac{20}{\pi+4}$

Thus, when $x=\frac{20}{\pi+4}$ then $\frac{d^{2} A}{d x^{2}}<0$.

Therefore, by second derivative test, the area is the maximum when length $x=\frac{20}{\pi+4} \mathrm{~m}$.

Now,

$y=5-\frac{20}{\pi+4}\left(\frac{2+\pi}{4}\right)=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} \mathrm{~m}$

Hence, the required dimensions of the window to admit maximum light is given by length $=\frac{20}{\pi+4} \mathrm{~m}$ and breadth $=\frac{10}{\pi+4} \mathrm{~m}$.