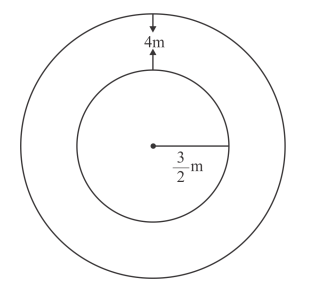
A well of diameter 3 m is dug 14 m deep.

We have,

Radius of well $r=\frac{3}{2} \mathrm{~m}$

Depth of well = 14 m

The volume of well

$=\pi \times\left(\frac{3}{2}\right)^{2} \times 14$

$=\pi \times \frac{9}{4} \times 14$

$=\frac{63}{2} \pi \mathrm{cm}^{3}$

Therefore,

Volume of earth dugout $=$ volume of well $=\frac{63}{2} \pi \mathrm{m}^{3}$

Let h be the height of embankment.

Clearly, embankment form a cylindrical shell whose inner and outer radius are

$\frac{3}{2} \mathrm{~m}$ and $\left(\frac{3}{2}+4\right)=\frac{11}{2} m$

Volume of embankment

$=\pi\left[\left(\frac{11}{2}\right)^{2}-\left(\frac{3}{2}\right)^{2}\right] \times h$

$=\pi\left[\frac{121}{2}-\frac{9}{4}\right] \times h$

$=\pi \times \frac{112}{4} \times h$

$=28 \pi \times h$

Volume of embankment = volume of earth dugout

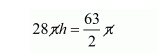
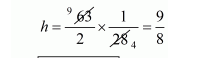
$h=1.125 \mathrm{~m}$

Hence, the height of embankment is 1.125 m